Piezo
Grundeigenschaften
Direkter Piezoeffekt (Generatorprinzip):
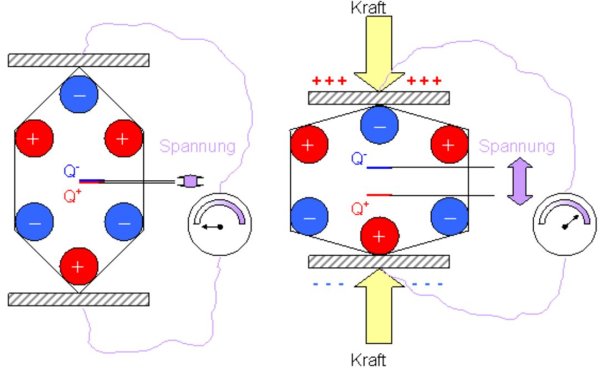
Der Piezo-Aktuator beruht auf den Piezoeffekt. Der direkte Piezoeffekt besagt, dass bei einer mechanischer Verformung durch Krafteinwirkung bestimmter nichtleitenden Materialien (in diesem Fall ein Kristall), ein elektrisches Feld E entsteht und somit aufgrund des Abstandes l eine elektrische Spannung U an der Materialoberfläche gemessen werden kann.
[ U = E \cdot l ]
Der direkte Piezoeffekt wird meistens in der Sensoranwendungen (Drucksensor) eingesetzt. Die erzeugte Spannung kann je nach dem als Mass für die Kraft oder Stauchung (Deformation) des Piezos verwendet werden. Wir der Piezo mit einer Zugkraft (sprich in entgegengesetzter Richtung) belastet, entsteht an deren Oberfläche eine negative (entgegengesetzte) Spannung.
 {.imgcenter}
{.imgcenter}
Indirekter Piezoeffekt (Aktorprinzip):
Der indirekte Piezoeffekt bewirkt das umgekehrte Phänomen. Beim Anlegen einer elektrischen Spannung an der Oberfläche des Kristalls, verformt sich dieser. Die Richtung der Verformung ist abhängig von der Polarität der angelegten Spannung und der Richtung des Vektors der Polarisation. Das Bewegungsausmass beträgt nur ein sehr kleiner Teil (1/1000-Bereich der Kristallabmessung). Daher können mit piezoelektrischen Aktoren im Vergleich zu anderen Technologien nur sehr kleine Hübe erzeugt werden und benötigen hohe Eingangsspannungen. Dafür ist deren Kraft (bis zu 30kN) und Dynamik (bis zu 10000 G) relativ gross. Weitere Vorteile sind die hohe Empfindlichkeit, die Verschleissfreiheit und die kurze Ansprechzeit.
Ausdehnung:
Die Ausdehnung eines Piezoaktors hängt von der Materialeigenschaft ab. Diese wird durch den Parameter Namens Piezomodul beschrieben. Dieser gibt die relative Verformung des Piezos an. Dabei gibt es zwei wichtige Piezomodule
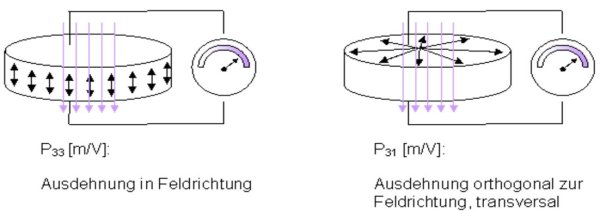
[ P_{33} [m/V]: \space Auslenkung \space in \space Feldrichtung \space (Longitudinaler \space Piezo-Effekt) ]
[ P_{31} [m/V]: \space Auslenkung \space orthogonal \space zur \space Feldrichtung \space (Transversaler \space Piezo-Effekt). ]
Die Breitenausdehnung steht orthogonal zur Feldrichtung der Spannung.
 {.imgcenter}
{.imgcenter}
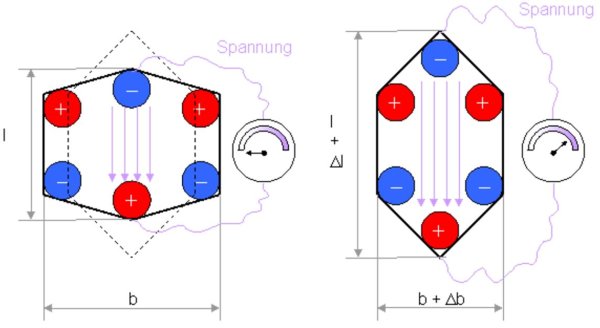
Man beachte, dass in der unteren Grafik die Änderung in Feldrichtung Dl positiv ist. Die Breitenänderung (orthogonal zur Feldrichtung) macht sich mit einem negativen Koeffizienten Db bemerkbar. Werden die Pole der Spannungsquelle vertauscht, ergibt sich eine Verformung mit positivem Db.
 {.imgcenter}
{.imgcenter}
Kraft:
[
F{max} \approx k{T} \cdot \Delta L_{0}
]
[ \Delta L_{0} \space [m]: \space max. \space freie \space Auslenkung \space ohne \space Belastung ]
[ k_{T} \space [N/m]: \space Aktorsteifigkeit ]
Maximale Kraft, die gegen eine unendlich steife Last (unendliche Federkonstante) erzeugt werden kann.
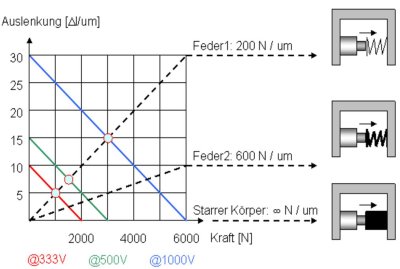
Die nächste Grafik zeigt bei verschiedenen Betriebsspannungen (1000V, 500V, 333V) die Krafterzeugung als Funktion der Auslenkung eines Piezotranslators mit einer nominalen Auslenkung von 30um/1000V und einer Steifigkeit von 200N/um. Die Punkte bestimmen die Kraft und Auslenkung für die jeweilige Aktor-Federkombination. Je steifer die Feder ist, desto weniger Auslenkung und desto mehr Kraft erzeugt der Piezoaktor. Bei einem starren Gegenstand (unendliche Federkonstante) mit einer unendlichen Steifigkeit erreicht der Piezoaktor seine maximale Kraft und seine kleinste Auslenkung (in diesem Fall Null). Die maximale Arbeit wird geleistet, wenn die Steifigkeit des Piezoaktors und der Feder gleich sind.
 {.imgcenter}
{.imgcenter}
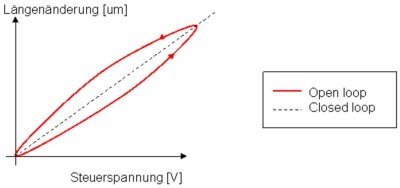
Hysterese:
Die Hysterese kommt bei spannungsgesteuerten Piezoaktoren zum Vorschein und kann durch verschiedene Methoden, beispielsweise wie bei einer Positionsregelung (closed loop) eliminiert werden. Die Hysterese hängt von der tatsächlichen Positionsänderung, nicht von der nominalen Auslenkung ab.
 {.imgcenter}
{.imgcenter}
Bauformen
Scheibe (Dickenschwinger):
Die Längenänderung L einer unbelasteten einzelnen Lage Piezokeramik kann mit der folgenden Gleichung abgeschätzt werden:
[ \Delta L = S \cdot L \approx \pm E \cdot \ d{ij} \cdot L{O} ]
[ S: \space Dehnung \space (relative \space Längenänderung \space \Delta L / L, \space dimensionslos) ]
[ L_{O} \space [m]: \space Keramiklänge ]
[ E \space [V/m]: \space elektrische \space Feldstärke ]
[ d_{ij} \space [m/V]: \space Piezomodul \space (Materialeigenschaften) ]
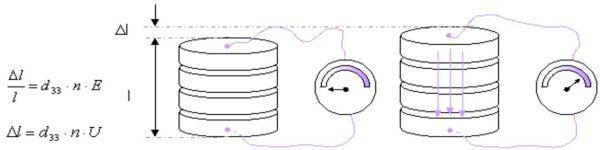
Stapel (Seriell):
Die Ausdehnung einer einzelnen Piezoscheibe ist sehr klein. Um den Stellweg zu vervielfachen, werden in den handelsüblichen Aktoren die Piezoscheiben gestapelt. Je dünner die Scheiben ausgeführt werden, desto höher ist bei gegebener Spannung die Feldstärke und somit auch die relative Längenänderung.
 {.imgcenter}
{.imgcenter}
Mit dieser Anordnung werden Stellwege im Bereich von 20um bis 1000 um und Kräfte bis zu 30kN erzielt.
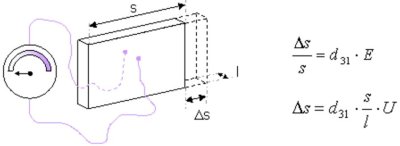
Streifenbauweise:
Bei der Streifenbauweise wird der transversale Piezoeffekt genutzt. Hier werden dünne Piezokeramik-Streifen parallel angeordnet. Deren Anzahl bestimmt die Steifigkeit des Aktors.
 {.imgcenter}
{.imgcenter}
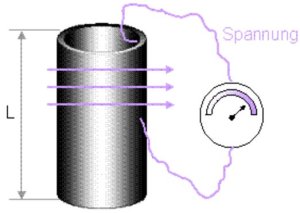
Tubus:
Axiale und radiale Dehnung
 {.imgcenter}
{.imgcenter}
Man beachte die Anschlusspunkte der elektrischen Spannung und des resultierenden Feldrichtungsvektors. Für die Berechnung der Längenausdehnung wir der Piezomodul d_31 verwendet, da die Längenausdehnung orthogonal zum Feldlinienvektor steht.
[ \Delta L \approx d_{31} \cdot L \cdot {U \over d} ]
[ \Delta L \space [m]: \space Auslenkung ]
[ d_{31} \space [m/V]: \space Piezomodul \space(Auslenkung \space orthogonal \space zur \space Polarisationsrichtung) ]
[ L \space [m]: \space Länge \space der \space Piezokeramik \space in \space Feldrichtung ]
[ U \space [V]: \space Betriebsspannung ]
[ d \space [m]: \space Dicke \space einer \space Keramiklage ]
Biegewandler (Bimorph):
 {.imgcenter}
{.imgcenter}
Biegescheibe (Disktranslatoren):
 {.imgcenter}
{.imgcenter}
Hybrid-Bauweise:
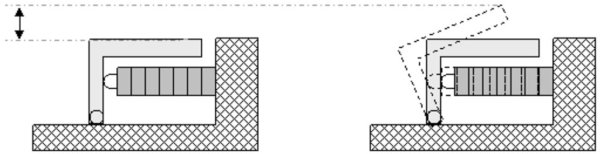 {.imgcenter}
{.imgcenter}
Aufbau und Funktionsweise
Übersicht:
| Kennwerte | Stapelbauweise normal | Stapelbauweise spezial | Streifenbauweise | Biegescheibe | Hybridbauweise | Einheiten |
|---|---|---|---|---|---|---|
| Nennstellweg | 6…70 | …90 | …45 | 50…200 | …100 | Um |
| Steifigkeit | 18…260 | …2000 | …15 | 0,15…0,3 | …1,4 | N/um |
| Eigenfrequenz | 6…50 | …50 | …13 | 1,1…2,5 | …2,2 | kHz |
| Druckbelastbarkeit | …1000 | …30000 | …450 | 20…50 | …50 | N |
| Zugbelastbarkeit | …100 | …3500 | …100 | …20 | …50 | N |
| Nennspannung | 150…1500 | …1500 | …1000 | …1000 | …1000 | V |
| Elektrische Kapazität | ….90 | …130 | …145 | 16…70 | …70 | nF |
Schaltungsarten
Keine
Vorspannung
Eine Vorspannung des Piezokristalles erfolgt dann, wenn ein Piezo innerhalb eines Bereiches sowohl gestaucht als auch gedehnt werden soll.
Kenngrössen
Der Piezo-Modul dij:
Der Kopplungsfaktor kij:
Der Kopplungsfaktor ist ein Mass für den Wirkungsgrad, mit dem die aufgebrachte elektrische Energie in mechanische Energie umgewandelt werden kann. Wie beim Piezo-Modul trägt auch dieser Wert ein Richtungsindizes i, j; er ist aber einheitenlos. Für Quarz beträgt der Kopplungsfaktor zum Beispiel k33=0,09.
Die Curie-Temperatur ϑ [°C]:
Oberhalb dieses Punktes verlieren Piezo-Keramiken ihre piezoelektrischen Eigenschaften. Das heisst, es gehen alle Materialeigenschaften verloren, die mit der Polarität verbunden sind.
Die Sättigungsdehnung Smax [um/m]:
Die Sättigungsdehnung gibt das Verhältnis der maximalen Längenänderung Δlmax zur Ausgangslänge L0 an. Sie liegt im Promillebereich und trägt üblicherweise die Einheit [μm/m].
Die Permittivitätszahl εij 17
Der thermische Ausdehnungskoeffizient α: Die thermische Stabilität von Piezokeramiken ist besser als die der meisten anderen Materialien (wie z.B. Stahl, Aluminium, ...). Sie wird durch den Ausdehungskoeffizienten α beschrieben, der die relative Längenänderung llΔ pro Kelvin spezifiziert. Er trägt die Einheit [μm/(mK)] = [Mikrometer/(Meter·Kelvin)], oft auch [1/K] = [K-1], und hat für PZT-Keramiken Werte im Bereich von α=2...9 μm/(mK).
Die Steifigkeit kT:
Grundsätzlich kann der Piezo-Aktor mit einem Feder-Masse-System verlgichen werden. Es kommen aber noch Abhängigkeiten von nichtlinearen Parametern hinzu. Eine belastete Piezokeramik erzeugt bakanntlich eine Ladung. Wenn dabei die Anschlüssen offen sind und die Ladung nicht abfliessen kann, entsteht eine innere Gegenkraft. Das heisst: eine Piezokeramik mit offenen Elektroden ist steifer als eine mit kurzgeschlossenen Elektroden. Wenn man bedenkt, dass ein Piezoaktor aus verschiedenen aktriven und passiven Materialien bestehen, wird die Situation noch komplizierter. Die Aktorsteifigkeit ist ein Wichtiger Parameter für die Berechnung der Resonanzfrequenz.
Die Resonanzfrequenz f0:
Die Resonanzfrequenz idealer Feder-Masse-Systeme berechnet sich aus:
[ f{0} = {1 \over 2 \pi} \cdot \sqrt{k{T} \over m_{eff}} ]
[ f_{0} \space [Hz]: \space Resonanzfrequenz \space des \space unbelasteten \space Aktors ]
[ k_{T}\space [N/m]: \space Aktor-Steifigkeit ]
[ m_{eff}\space [kg]: \space effektive \space Masse \space (ca. \space 1/3 \space der \space Masse \space der \space Piezokeramik \space plus \space evtl. \space End-stücke) ]
Bei Positionieraufgaben werden Piezo-Aktoren deutlich unterhalb der Resonanzfrequenz betrieben, da die praktische Resonanzfrequenz aufgrund von Unlinearitäten nicht immer mit der obigen idealen Gleichung übereinstimmt.
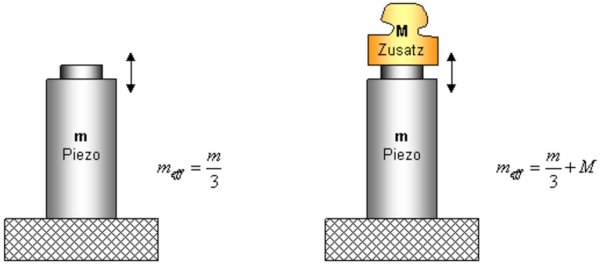
Die in den Datenblättern aufgeführten Angaben zu der Resonanzfrequenz beziehen sich immer auf den unbelasteten, an einer Seite befestigten Aktor. Kommt eine Zusatzmasse hinzu, so reduziert sich die Resonanzfrequenz.
[ f{0}' = f{0} \cdot \sqrt{m{eff} \over m{eff} + M} ]
[ M \space [kg]: \space Zusatzmasse ]
Das untenstehende Bild zeigt das Masseverhalten im unbelasteten und belasteten Fall.
 {.imgcenter}
{.imgcenter}
Kräfte durch Vorspannfedern haben keinen entscheidenden Einfluss auf die Resonanzfrequenz.
Die Blockierkraft (maximale Stellkraft):
Die Blockierkraft wird bei einem Aktor erreicht, wenn er gegen einen unendlich steifen Körper Aufbau eingespannt ist.
Ansteuerung
Angesteuert werden die Piezoaktoren mit einer Spannung. Diese bewegt sich je nach Piezotyp zwischen 10 und 1000 Volts. Als Treiber für den Piezoaktor kann eine beliebige Spannungsquelle verwendet werden. Bei geregelten Positionierungen wird der Treiber von einer Positionsregelung geführt. Rausch- oder Störanteile in der Ansteuerungsleitung, die sich frequenzmässig im Bereich der Resonanzfrequenz des Aktors befinden, bewirken eine merkliche Störung der Piezoverformung. Die Hersteller von Piezoaktoren bieten ganze Regelgeräte an, mit denen sogar vorgegebene Bahnen abgefahren werden können.
Anwendungsgebiete
Massenspeicher
Halbleiter- und Mikroelektronik
Präzisionsbearbeitung
Life Science, Medizintechnik
Optik, Photonik und Nanometrologie
Beispiele:
Aktive Vibrationsdämpfung
Halbleiter- und Mikroelektronik (Positionierung von Wafer)
Werkzeugsjustage
Ventilsteuerung
Linearantriebe
Bildstabilisierung
Literaturhinweise
- www.pi.ws Physikinstrumente, Tutorium Piezoaktorik und Nanopositionierung
- Mechatronik Komponenten Methoden Beispiele, ISBN 3-446-40599-2
Verbindungsmöglichkeiten Piezo-Aktor
| Sensortyp | Bemerkung zur Kombination |
|---|---|
| Kapazitiv | Kann im Bereich der Drehzahlmessung oder zur Ermittlung einer Endanschlagsfahrt verwendet werden. Für eine direkte lineare Messung muss auf die Nichtlinearität des Sensors geachtet werden. Dieser Sensor eignet sich auch für statische Anwedungen. |
| Induktiv | Kann im Bereich der Drehzahlmessung oder zur Ermittlung einer Endanschlagsfahrt verwendet werden. Für eine direkte lineare Messung muss auf die Nichtlinearität des Sensors geachtet werden. Dieser Sensor eignet sich auch für statische Anwedungen. |
| Magnetostriktiv | Es können Auflösungen bis zu 1um gemessen werden. Typischerweise besitzen magnetostriktive Sensoren lineare Messwege ab von 25mm bis zu 7600mm. |
| Piezo | Bei dynamischen Anwendungen kann der Piezo als Messglied verwendet werden. Es kann der Selbe Typ von Piezo-Aktor verwednet werden. |
| Potentiometrisch | Einget sich für grosse Hübe gut für lineare Bewegungen als Absolutpositionsgeber. Bei kleinen Auslenkungen wie beim Piezoaktor, kann es zu Auflösungseinbüssungen kommen. Bei rotativen Bewegungen kann der Drehgeber nicht beliebige Umdrehungen in der selben Richtung ausführen. |
| DMS | Nicht geeignet. |
| Fotoelektrisch | Kann sowohl für Drehzahlmessungen, als auch für linearer absoluter Positionsgeber eingesetzt werden. |
| Ultraschall | Bei akustischen Systemen kann mit einer Aufslösung von 0.3mm gerechnet werden. Für hochdynamische Anwendungen eher nicht geeignet. |
| Magnetisch |
Verbindungsmöglichkeiten Piezo-Aktor
| Controllertyp | Bemerkung zur Kombination |
|---|---|
| ASIC | Kann über eine Leistungselektronik oder Treiber angesteuert werden. |
| SPS | Eher unübliche Kombination. |
| Prozessrechner | Kann über eine Leistungselektronik oder Treiber angesteuert werden. |
| Microcontroller | Kann über eine Leistungselektronik oder Treiber angesteuert werden. |
| Industrie-PC | Kann über eine Leistungselektronik oder Treiber angesteuert werden. |
Verbindungsmöglichkeiten Piezo-Aktor
| Identifikationstyp | Bermerkung zur Kombination |
|---|---|
| Barcode | Zurzeit keine Kombination bekannt. |
| 2D-Code | Zurzeit keine Kombination bekannt. |
| RFID | Zurzeit keine Kombination bekannt. |
| Magnetisch | Zurzeit keine Kombination bekannt. |
| Bildverarbeitung | Zurzeit keine Kombination bekannt. |
| Elektro-Mechanisch | Zurzeit keine Kombination bekannt. |
Verbindungsmöglichkeiten Piezo-Aktor
| Kommunikationstyp | Bemerkung zur Kombination |
|---|---|
| ASI | Kommuniziert in der Regel über den ASI-Bus mit einer SPS. Dabei werden hauptsächlich binäre und durch Erweiterungen auch analoge Werte übertragen. |
| CAN | Mit einer digitalen Schnittstelle können die Daten über einen CAN-Bus weitergeleitet werden. Somit bleiben grosse Kabelbäume erspart. |
| Profibus | Mit einer digitalen Schnittstelle können die Steuerdaten über einen Profibus weitergeleitet werden. Vor allem ürsprünglich analoge Signale können ohne Einflüsse wie Spannungsabfall oder Induzierte Spannungen über weite Distanzen trasportiert werden. |
| Industrial Ethernet / Profinet | Mit dem industrial Ethernet können Steuersignale über grosse Distanzen transportiert werden. Somit können Aktoren ferngesteuert und ferngewartet werden. |